
Learn Recursion Without Wanting to Shoot Yourself
A practical self-help guide.
Raise you're hand if this is you. You've been a hard-working, scrappy professional developer for a number of years. Over these years, you've learned by doing. You've managed to create real, useful things. You've regularly handled deluges of uncertainty. You've taken full responsibility for finding tangible, working solutions to critical problems. You've locked yourself in rooms and paced, inhaling stimulants and exhaling expletives, brutally iterating until things finally, finally worked.
You should, if you really looked objectively, be reliably proud of yourself. Reliably confident. You should be assured in your identity and craft, as a brave and experienced coder clutching a bundle of metaphoric digital purple hearts.
But, you aren’t. Because you feel deep down that you aren’t a “real” programmer. Because real programmers understand — fully, deeply, nonchalantly yet indisputably — things like recursion.
It’s not that you don’t get the rough idea and all. Frames within frames within frames? Turtles all the way down? Yes. You nod at the technical buzzwords and giggle at the programming memes. But when you sit down to solve a real-life problem with code and start considering implementations, you… swear under your breath and begin typing out another f***ing for loop.
And here’s the thing: for loops are generally just fine. Most meaningful success from coding really does come more from tenacity and careful planning than from dazzling our fellow under-the-hood jockeys. In tech, straightforward is better than magical.
But mastery of slightly more sophisticated CS concepts like recursion offer much more than feeling 50% more at ease before a technical interview. Inevitably, there will be times when we do need some magic. Sometimes the fancier solution is simply the right answer. In these situations, we must be careful not to let a Keep It Simple Stupid mentality hijack our thinking too far in the other direction. Moreover, these concepts help keep our craft exciting and fresh, and keep our problem-solver brains from stagnating around old patterns.
So, let’s dig in and see what we can unearth. Let’s first figure out what recursion is in simplest terms. Then, let’s cover common implementation patterns, and what those implementations look like in working code. Finally, let’s cover how to think about what actually happens when recursion performs its magic.
What Is Recursion?
The best practical definition of recursion I’ve heard comes from Mattias Petter Johansson’s superb video on the subject, as it is dead simple while remaining concrete:
Recursion is when a function calls itself until it doesn’t.
In my experience, if someone encounters a new concept and finds it a struggle, it is less that they are not able to grasp the idea and more that it isn’t clear why the idea is useful. This is certainly true for me, and recursion was no exception.
When I first heard the definition, I recognized it as the endless mirrors meme that almost everyone has seen. I tried to think about what this would look like as code.
function reflect(image) {
// but how do you stop?
return reflect(image); // what is the point?
}
Uhh, hmm. Okay. I had many questions. Why would anyone ever do this? And how would it know when to stop calling itself? An arbitrary counter? And isn’t the cardinal sin of explaining what a word means to use the word in your explanation? It didn’t seem practical. It seemed like theory for theory’s sake.
The whole thing felt somehow fundamentally nonsensical, counterintuitive, and on an outside chance might possibly cause the universe to implode.
The Moment of Forehead-Smacking
I visualized the endless mirrors again, and after some marinating it hit me my code representation was missing something crucial: the mirrors were shrinking the image slightly with each reflection. In other words, in code terms, the function must call itself with an updated argument each time.
function reflect(image) {
image.size = image.size - 1;
// same `reflect()` but updated `image`
return reflect(image);
}
This also explained how to stop the otherwise endless call loop.
function reflect(image) {
image.size = image.size - 1;
// ah, HERE's how we stop.
if (image.size == 0)
return image;
return reflect(image);
}
Oooooohhhhhhhh. Everything started to make sense. Is there any dopamine rush sweeter than that of a spontaneous eureka moment? I’ll fight anyone who says there is.
So, at the risk of flagrantly tramping over elegance in the service of being explicit, I’ll augment MPJ’s definition:
Recursion is when a function calls itself with an updated argument each time until a condition is satisfied.
For me, this was a key insight: just as with taking repeated bites of an apple, calling the same function over and over with new arguments isn’t actually repeating yourself. Rather, you are performing the same action on a continuously evolving object that is carrying you towards a desired outcome.
And this, it turns out, has real practical power.
Real Life Patterns
This is the part that gave me that internal deer-in-headlights feeling for so many years, every time I sat down to solve an actual problem. It is all well and good to gesticulate excitedly about theory, but nuts-and-bolts implementation is the master we serve. And implementation is almost always the tougher master. When pressed against a corner by real-world challenges and deadlines, I tend to throw my hands up and reach for what I already know.
It turns out though, that buried beneath the fanciness, recursion implementations follow a simple and fairly reliable set of patterns. These are the two that I see most often, and that I’ve learned to rely upon during “actual” coding.
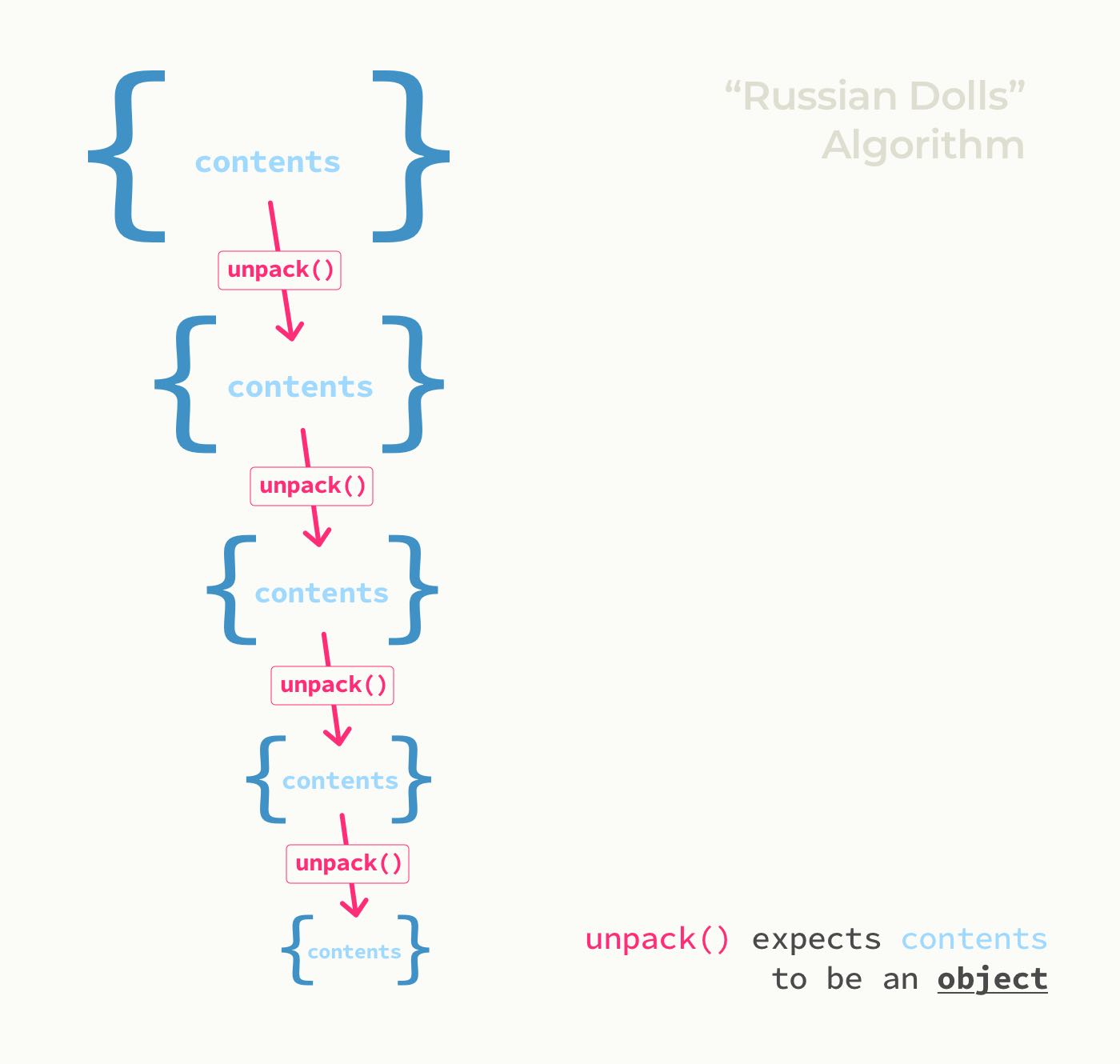
Pattern 1: The Russian Dolls

The Russian doll metaphor is one of the “classic” recursion examples, and it is a good one. This being the internet, you’ll understand that one or more of our dolls are legally required to be anthropomorphic cats. Also, playing with dolls is probably a bit anachronistic. Perhaps “pay homage to the leisure activities of a deceased and once-great ancient civilization” is more appropriate.
Ahem, so when you want to take the dolls out to pay homage to the leisure activities of a deceased and once-great ancient civilization, you unpack them and line them up side-by-side, as above. When you put them away, the dolls all fit nicely inside one another, so that from the outside one only sees the biggest one.
Here are our Russian cat-dolls in this put-away state, represented as a data structure.
// Ivan is the mouse
const catDolls = {
name: "Katerina",
inside: {
name: "Dimitri",
inside: {
name: "Alyosha",
inside: {
name: "Grushenka",
inside: {
name: "Ivan",
inside: null
}
}
}
}
}
Notice how for a structure like the dolls above, a traditional loop would only “see” it as one item. Yet functionally, it is not — our human mind clearly understands it to be a repeating pattern, and we want to iterate on it. This is where recursion rides in on its shining golden rainbow pegasus.
Tunneling To the Center
Recursion is an amazing tool for operating on data structures with depth or nesting. Recursive patterns allow us to easily “drill down” into data structures, instead of “skimming across” them like for loops do. Recursion lets us easily iterate into something instead of across it.
Enough with the wild claims, though. Let’s see some hard evidence.
Here’s a recursive function to unpack our cat-dolls into a simple array:
let unpackedDolls = [];
function unpack(doll) {
// add the current doll to our array.
unpackedDolls.push(doll.name);
// if nothing inside the doll, we are done
if (!doll.inside)
return doll;
// re-run with modified argument
let nextDoll = doll.inside;
return unpack(nextDoll) // ding ding! recursive call here
}
unpack(catDolls);
Look familiar? Like the earlier endless mirrors code, this function a) modifies the argument and re-runs itself with it during each loop, and b) checks the argument against a base case to see if it should break the loop.
The part that is new — and incidentally what nudges it towards being actual, productive code — is the first line, where we snag each doll name for the unpackedDolls array. In other words, it’s where we leverage our loop to do meaningful work of some kind.
This gives us a generic pattern with three basic components:
- Do meaningful work. Extract to an external array, print to console, etc.
- Check for the base case. Without this, our loop will careen on infinitely until we hit a wild
StackOverflowError. - Modify the argument and re-run the function with it. Hopefully, self-explanatory at this point.
Or the same thing expressed as pseudo-code:
function doSomething(argument) {
// 1. DO MEANINGFUL WORK with current argument:
// extract it to an external array, print it to console, etc.
doStuffWith(argument);
// 2. TEST FOR "BASE CASE" or "catcher" condition, which
// if true returns the argument without recursion.
if (nothingMoreToDo(argument))
return argument;
// 3. MODIFY THE ARGUMENT, then
// re-run the function with the new argument.
let modified = modify(argument);
return doSomething(modified); // recursive call!
}
Note that the ordering of these components is arbitrarily swappable depending on particulars, with the possible exception of the recursive call generally occurring at the end.
Just to widen perspective a bit, here is an even more bone-head use case.
// Count to ten.
function countUp(num) {
// do meaningful stuff
console.log(num);
// base case
if (num == 10)
return num;
// re-run with updated argument
let newNum = num + 1;
return countUp(newNum);
}
countUp(0); // 1 2 3 4 5 6 7 8 9 10
Encapsulation
In the cat-dolls example, you may have noticed that defining the unpackedDolls array outside the function was a bit awkward. Specifically, it’s not so great that the “collector” arrays get populated as a side effect — intuitively the function should return the array itself when invoked.
We are forced into this pattern because any variables we initialize inside a recursive function will turn to vapor at the next iteration. In other words, the body of a recursive function operates the same as the body of a for loop.
So, this won’t work…
function count(num) {
let counted = []; // !! paved over with each iteration
counted.push(num)
if (num <= 10)
return num;
return count(num + 1);
}
count(0);
…for the same reason this won’t work:
for (num = 1; num <= 10; num++) {
let counted = []; // !! paved over with each iteration
counted.push(num);
}
The for loop version of this is everywhere, and it gets handled everywhere by properly moving counted outside the loop so it isn’t paved over, then encapsulating the whole thing in a function call.
function countToTen(start) {
let counted = []; // persists through the loop!
// begin loop
for (num = start; num <= 10; num++) {
counted.push(num);
}
// end loop
return counted;
}
countToTen(1); // [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
There, nice and tidy. This might seem eye-rollingly obvious but hang tight, the point is we do this with recursion too.
The recursive version of this might seem more sophisticated on first glance because it has a function within a function, but it is the exact same pattern done for the exact same reasons.
function countToTen(start) {
let counted = []; // persists through the (recursive) loop!
// begin loop
function count(num) {
counted.push(count)
if (num <= 10)
return num;
return count(num + 1);
}
count(start);
// end loop
return counted;
}
countToTen(1); // [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
Back to our dolls. This pattern works exactly the same for them.
function collectDolls(dolls) {
var collected = []; // persists!
function unpack(doll) {
collected.push(doll.name);
if (!doll.inside)
return doll;
return unpack(doll.inside)
}
unpack(dolls);
return collected;
}
collectDolls(catDolls);
// ["Katerina", "Dimitri", "Alyosha", "Grushenka", "Ivan"]
This encapsulation now gives us a pure function without side effects, which is pretty great. Things are starting to look kinda useful.
Still, we are fairly limited — this pattern will only work with nested structures that deal with one object at a time. In other words, we can only drill straight down. Roughly speaking, we have traditional loops to traverse horizontally, and now recursive loops to traverse vertically. But what about the ability to do both? How do we handle nested lists of objects?
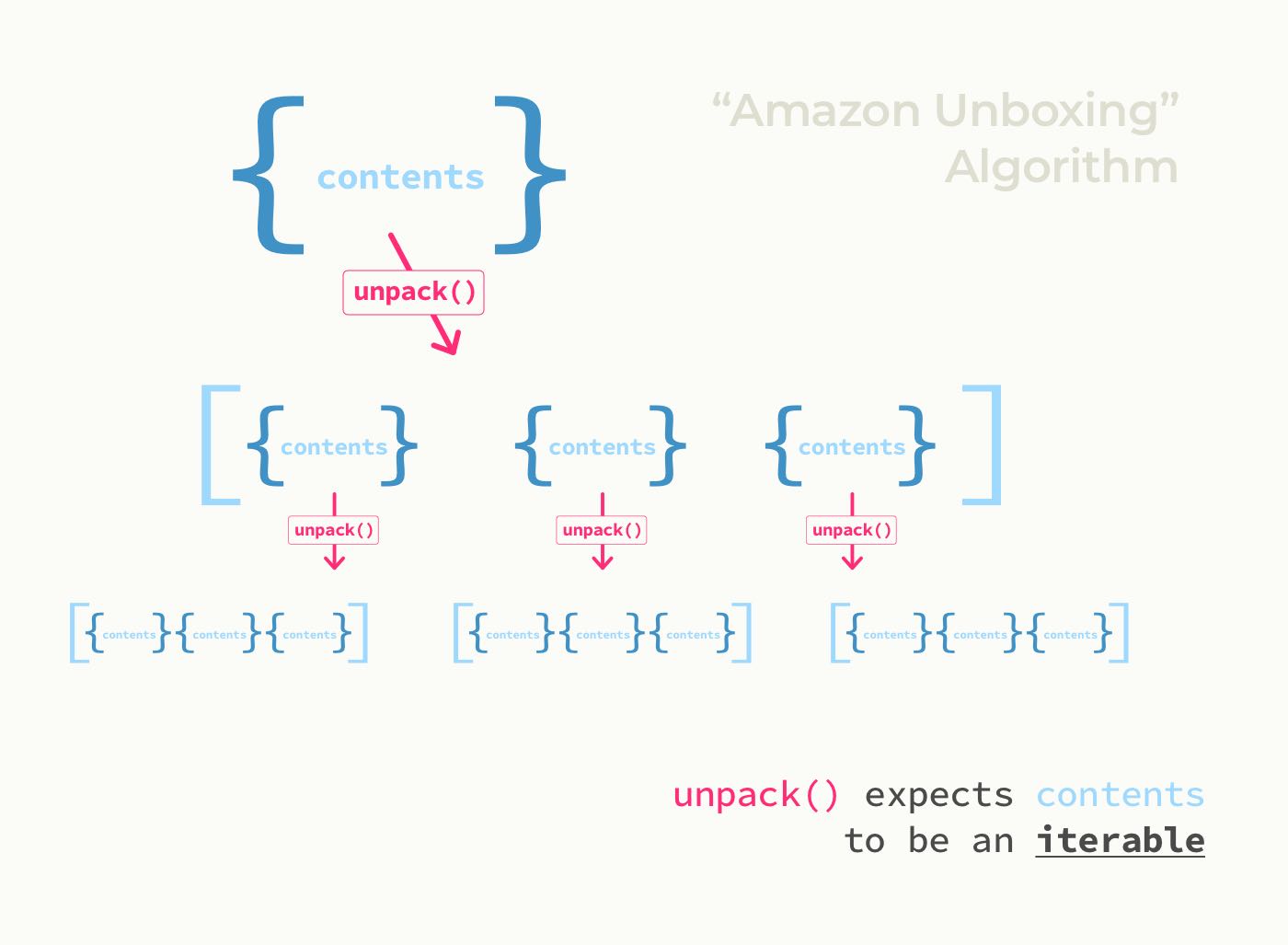
Pattern 2: Amazon UnBoxing

Okay, it’s real-life analogy time again.
Imagine you receive two packages from Amazon. Now, you order a lot of stuff from Amazon, so you have no idea what’s in the packages, but it’s hardly a problem — your brain has a comfortable routine for opening them and getting at the happy treasures within them. You tear open the first one and discover whiskey-scented pillar candles. Sweet. First giddy consumerism high of the day. You tear open the second one and discover… three smaller boxes. OH GOD. This was not the expected results! What shall we do????
Yet you know, dear Reader, that were you in this situation there would be no panic. You wouldn’t think twice about it — you would simply execute your brain’s open Amazon package routine on the three smaller packages. If there are even smaller packages inside those, that’d be fine too (not to mention adorably, whimsically surreal). You would simply keep going until you hit the paydirt of an actual ordered product.
At first glance, we might etch this out in code like this:
function unpack(box) {
let contents = box.contents;
if (isActualProduct(contents)) {
return contents
}
else {
return unpack(contents);
}
}
Looks familiar, right? This is simply the Russian dolls algorithm again. But, there’s a significant problem. As mentioned, the above will only work if there is a single box inside each larger box.
This, of course, would be pointless — the whole reason for a larger box is to carry multiple smaller boxes inside. In that scenario, that means box.contents above will be an array.
Let’s explore what this might look like in code. Here is an Amazon Prime delivery of a large and a small mystery box in data structure form.
// Don't judge me.
const smallBox = { contents: ["scented candles"] };
const largeBox = { contents: [
{ contents: ["stuffed giraffe", "stuffed polar bear"]},
{ contents: ["sewing thread", "sewing needle"]},
{ contents: ["power drill"]}
]}
Notice that the actual products in each box are nested in an array. This means each time we unpack a box and find its contents, we must begin by iterating across those contents.
// tiny helper function for legibility
const isProduct = (item) => typeof(item) == "string";
let products = []; // our collector array
function unpack(box) {
// start by iterating over the expected array
box.contents.forEach(item => {
// now apply our normal components for each item
if (isProduct(item)) { // CHECK BASE CASE
products.push(item); // DO MEANINGFUL WORK
return;
}
return unpack(item); // RE-RUN W NEW ARG
})
}
You’ll notice our three basic recursion components still apply here, but now they are all happening inside a traditional array loop.
This means we are actually now running two loops that work together: a “vertical” recursive loop that progresses layer-by-layer deeper into the object, and a “horizontal” array loop that scours across each layer upon arrival. Because of this, this function now not only drills down but also fans out.
Pretty sweet. Let’s generalize this as pseudo-code like we did for the Russian dolls:
function doSomething(object) {
// 1. EXPECT SOME ITERABLE that we can loop across:
object.contents.iterate(child => {
// 2a. DO MEANINGFUL WORK
doStuffWith(child);
// 2b. TEST FOR "BASE CASE"
if (nothingMoreToDo(child))
return child;
// 2c. MODIFY THE ARGUMENT THEN RE-RUN
let modified = modify(child);
return doSomething(modified); // recursive call!
})
}
This cooperative across-and-down pattern allows us to write functions that handle all kinds of uncertainties in the topology of our data, with relatively little code.
Here is another common use case example:
// flatten a randomly nested series of arrays.
const nested = [1, 2, [3, [4, [5, 6, 7], 8]], 9, [10]];
let flattened = []; // collector
function flatten(array) {
array.forEach(item => { // iterate
// base case
if (!Array.isArray(item)) {
flattened.push(item); // meaningful work
return;
}
return flatten(item); // child item is an array -- re-run.
})
}
flatten(nested);
flattened; // [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
Note that nested could be as few or as many layers as is required, and in any permutation. Moreover, we don’t need to know anything about that permutation beforehand, other than the fact that they are all arrays.
Recursion + Reduce = Happy
It’s worth noting that the type of loop does not have to be forEach() — you could use map(), reduce(), a straight for loop, etc. It simply depends on the particulars of the situation and your own preference.
It is particularly common to see this pattern implemented with reduce(), which slims things down quite a bit in a quasi-voodoo-magic-seeming way.
Here is reduce() applied to Amazon unboxing:
function unpack(box) {
return box.contents.reduce((products, child) => {
if (isProduct(child)) { // CHECK BASE CASE
return products.concat(child); // DO MEANINGFUL WORK
}
return products.concat(unpack(child)); // RE-RUN W NEW ARG
}, [])
}
And here our flattening of arrays:
function flatten(array) {
return array.reduce((flattened, item) => {
if (!Array.isArray(item)) {
return flattened.concat(item);
}
return flattened.concat(flatten(item));
}, [])
}
I’ll refrain from turning this into a full tutorial on reduce(), but notice that our “collector” arrays, products and flattened, are no longer initialized outside the function. Instead, they “magically” appear as an argument to the function passed to reduce(). This is actually reduce’s primary purpose — to abstract and handle this common “do stuff with each item of an array and add the results to some sort of collector” pattern.
If you’d like to learn more about reduce() used specifically with recursion, I highly recommend this concise and friendly article by developer / entrepreneur Vicky Lai. For reduce() in general, check out MPJ’s series on functional programming.
Mechanics Etc.
At this point, it is my hope that you feel a little less daunted with implementing some basic recursive patterns in your own code. Before we wrap, however, I want to address one final area that was a source of cognitive dissonance for me — what is actually happening behind the scenes when a recursive loop runs.
Dirty Dishes
A declared function is like a user manual — a set of instructions describing how to do something. It lays out the procedure to accomplish a given task. When a function is called, however, it becomes like an item on a to-do list. It is not instructions, but rather a task that must be completed sometime in the future. And just like human to-do list tasks, these called functions can quickly amass into a stressful pile.
In computer programs, this pile is called the call stack.
An easy way to visualize the call stack is as a pile of dirty dishes. Each dirty dish is a called function. Each different type of crusty food residue is a function argument. Imagine you are a dishwasher in a restaurant, and servers swoop back into the airless kitchen in a hurried stream, unceremoniously dropping more dishes on your pile. New dishes are added in clumps as full tables are cleared, but you attend to them one at a time, in order. It seems like you can never quite get to the bottom, like you can never wash them quite fast enough. Finally, mercifully, the rush of customers slows as the dinner hours fade and you at last get completely through your stack. Whew. At least you have headphones, history podcasts, and Spotify.
Not to bring us near the newly uncomfortable area of machine serfdom ethics, but this is the experience our program interpreters have when we run programs. The key point of this allegory is that your functions are attended to one at a time, in order, no matter how complicated the manner in which they were called. A restaurant kitchen is pure orchestrated chaos, but the dishes are always done one at a time.
Recursion on the Call Stack
This fact is especially salient with recursive function patterns, where up to now our intuitions have been orbiting around ideas of nesting, drilling into, and one thing inside another. None of these are particularly evocative of a single, ordered stack.
Yet behind the scenes, a single, ordered stack they are.
Let’s return all the way back to our initial example of the endless mirrors, and this time watch the call stack rise and fall.
const myFace = {
size: 3,
hair: null,
description: "a budget Ed Norton from the 90s"
}
function reflect(image) {
image.size = image.size - 1;
// pretend we are doing something meaningful here
// like display the image
if (image.size == 0)
return image;
return reflect(image);
}
reflect(image); // { size: 0, ... }
The key to intuition around this found in the recursive return statements. Specifically, in two things:
returnmeans return control to the thing that called you.returnwill WAIT until any function call to its right has completed.
In other words, whenever you see a line like return someFunction(), it means that someFunction() must complete before the return bit actually happens.
In the above mirrors example, this would play out at runtime something like this:
reflect({ size: 3 })
// size isn't zero, so WAIT for result from...
reflect({ size: 2 })
// size isn't zero, so WAIT for result from ...
reflect({ size: 1 })
// size IS zero, so...
return { size: 0 }
// `reflect({ size: 2 })` DONE WAITING!
return { size: 0 }
// `reflect({ size: 3 })` DONE WAITING!
return { size: 0 }
You can see this sort of cascade-in-then-out shape that occurs, which hints at what is happening behind the scenes.
Each reflect() call shrinks image a bit, calls itself again with the shrunken image, then waits for the result before finally returning. So size: 3 can’t complete until size: 2, which can’t complete until size: 1.
Then, success happens — size: 1 hits our base case of zero and returns it directly, without needing to wait for anything. The result is passed rapidly back up the chain to everyone else, who have already done their required work and are just waiting around so they can finally finish their return statement.
We can imagine this in terms of our dishwasher analogy as a formal dish set. Like anything else in the pile, each dish in the set must be washed individually, in order. However, since the smaller dishes must rest on top of the larger ones, we can’t cede the larger dishes in the set to the cooks until the smaller ones are washed too.

So, with recursive patterns, we always have these two waves of action. The first ripples inward as a function continuously calls itself towards some base case. This is typically where all the “real work” happens. Then, a second wave ripples back outward when the base case is found and is quickly passed up the chain to the outermost call.
Conclusion
Recursion is both a powerful way of thinking and a design pattern that is particularly well suited to problems or data structures with depth or nesting. When combined with more “traditional” iteration, recursive patterns can often flexibly handle a wide variety of data permutations with relatively little code. Finally, the mechanics behind recursion can be understood first by understanding the call stack, and how — like a dishwasher in a restaurant kitchen — functions are handled in strict single-file line at runtime, no matter how convoluted or nested the function declarations may appear.
If you chose to stay with me through what has ended up to be a pretty long-ass read, I am deeply grateful. I hope some, all, or any of this material may have helped you to develop more intuition and burn away some of the fog around these concepts.
As I alluded to earlier, it’s hard for me to imagine a better feeling that the empowerment and excitement of an aha moment, where something that historically has been intimidating and out of reach suddenly lands on your front doorstep, ready to be your loyal and stalwart companion for the rest of time.
I hope this article was able to aid you in reaching one more such moment.